The t-Test

As we have seen throughout this book, many studies in psychology focus on the difference between two means. The most common null hypothesis test for this type of statistical relationship is the t‐ test. In this section, we look at three types of t tests that are used for slightly different research designs: the one- sample t‐test, the dependent-samples t‐ test, and the independent-samples t‐ test. You may have already taken a course in statistics, but we will refresh your statistical knowledge.

One-Sample t-Test

The one-sample t‐test is used to compare a sample mean (M) with a hypothetical population mean (μ0) that provides some interesting standard of comparison. The null hypothesis is that the mean for the population (µ) is equal to the hypothetical population mean: μ = μ0. The alternative hypothesis is that the mean for the population is different from the hypothetical population mean: μ ≠ μ0. To decide between these two hypotheses, we need to find the probability of obtaining the sample mean (or one more extreme) if the null hypothesis were true. But finding this p value requires first computing a test statistic called t. (A test statistic is a statistic that is computed only to help find the p value.)

The reason the t statistic (or any test statistic) is useful is that we know how it is distributed when the null hypothesis is true. In this case, the distribution is unimodal and symmetrical, and it has a mean of 0. Its precise shape depends on a statistical concept called the degrees of freedom, which for a one-sample t-test is N − 1. The important point is that knowing this distribution makes it possible to find the p value for any t score.

Fortunately, we do not have to deal directly with the distribution of t scores. If we were to enter our sample data and hypothetical mean of interest into one of the online statistical tools or into a program like SPSS (Excel does not have a one-sample t‐test function), the output would include both the t score and the p value. At this point, the rest of the procedure is simple. If p is equal to or less than .05, we reject the null hypothesis and conclude that the population mean differs from the hypothetical mean of interest. If p is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say that the population mean differs from the hypothetical mean of interest. (Again, technically, we conclude only that we do not have enough evidence to conclude that it does differ.)

Thus far, we have considered what is called a two-tailed test, where we reject the null hypothesis if the t score for the sample is extreme in either direction. This test makes sense when we believe that the sample mean might differ from the hypothetical population mean but we do not have good reason to expect the difference to go in a particular direction. But it is also possible to do a one-tailed test, where we reject the null hypothesis only if the t score for the sample is extreme in one direction that we specify before collecting the data. This test makes sense when we have good reason to expect the sample mean will differ from the hypothetical population mean in a particular direction.

Here is how it works: We simply redefine extreme to refer only to one tail of the distribution. If 5% of the values of t beyond the critical value for t are all in one tail of the distribution, the advantage of the one-tailed test is that critical values are less extreme. If the sample mean differs from the hypothetical population mean in the expected direction, then we have a better chance of rejecting the null hypothesis. The disadvantage is that if the sample mean differs from the hypothetical population mean in the unexpected direction, then there is no chance at all of rejecting the null hypothesis.

Example: One-Sample t–Test

Imagine that a health psychologist is interested in the accuracy of university students’ estimates of the number of calories in a chocolate chip cookie. He shows the cookie to a sample of 10 students and asks each one to estimate the number of calories in it. Because the actual number of calories in the cookie is 250, this is the hypothetical population mean of interest (µ0). The null hypothesis is that the mean estimate for the population (μ) is 250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the participants’ actual estimates are as follows:

250, 280, 200, 150, 175, 200, 200, 220, 180, 250.

The mean estimate for the sample (M) is 212.00 calories and the standard deviation (SD) is 39.17. The health psychologist can now compute the t score for his sample. If he enters the data into one of the online analysis tools or uses SPSS, it would tell him that the two- tailed p value for the computed t score (with 10 − 1 = 9 degrees of freedom) is .013. Because this is less than .05, the health psychologist would reject the null hypothesis and conclude that university students tend to underestimate the number of calories in a chocolate chip cookie.

Finally, if this researcher had gone into this study with good reason to expect that university students underestimate the number of calories, then he could have done a one-tailed test instead of a two-tailed test. The only thing this decision would change is the critical value, which would be −1.833. This slightly less extreme value would make it a bit easier to reject the null hypothesis. However, if it turned out that university students overestimate the number of calories—no matter how much they overestimate it—the researcher would not have been able to reject the null hypothesis.

The Dependent-Samples t–Test

The dependent-samples t-test (sometimes called the paired-samples t‐test) is used to compare two means for the same sample tested at two different times or under two different conditions. This comparison is appropriate for pretest-posttest designs or within-subjects experiments. The null hypothesis is that the means at the two times or under the two conditions are the same in the population. The alternative hypothesis is that they are not the same. This test can also be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.

It helps to think of the dependent-samples t‐test as a special case of the one-sample t‐test. However, the first step in the dependent-samples t‐test is to reduce the two scores for each participant to a single difference score by taking the difference between them. At this point, the dependent-samples t‐test becomes a one-sample t‐test on the difference scores. The hypothetical population mean (µ0) of interest is 0 because this is what the mean difference score would be if there were no difference on average between the two times or two conditions. We can now think of the null hypothesis as being that the mean difference score in the population is 0 (µ0 = 0) and the alternative hypothesis as being that the mean difference score in the population is not 0 (µ0 ≠ 0).

Example: Dependent-Samples t–Test

Imagine that the health psychologist now knows that people tend to underestimate the number of calories in junk food and has developed a short training program to improve their estimates. To test the effectiveness of this program, s/he conducts a pretest-posttest study in which 10 participants estimate the number of calories in a chocolate chip cookie before the training program and then again afterward. Because s/he expects the program to increase the participants’ estimates, s/he decides to do a one-tailed test. Now imagine further that the pretest estimates are:

230, 250, 280, 175, 150, 200, 180, 210, 220, 190

and that the posttest estimates (for the same participants in the same order) are:

250, 260, 250, 200, 160, 200, 200, 180, 230, 240.

The difference scores, then, are as follows:

20, 10, −30, 25, 10, 0, 20, −30, 10, 50.

Note that it does not matter whether the first set of scores is subtracted from the second or the second from the first as long as it is done the same way for all participants. In this example, it makes sense to subtract the pretest estimates from the posttest estimates so that positive difference scores mean that the estimates went up after the training and negative difference scores mean the estimates went down.

If s/he enters the data into one of the online analysis tools or uses Excel or SPSS, it would output that the one-tailed p value for this t score (again with 10 − 1 = 9 degrees of freedom) is .148. Because this is greater than .05, s/he would retain the null hypothesis and conclude that the training program does not significantly increase people’s calorie estimates.

The Independent-Samples t-Test

The independent-samples t‐test is used to compare the means of two separate samples (M1 and M2). The two samples might have been tested under different conditions in a between-subjects experiment, or they could be pre-existing groups in a cross-sectional design (e.g., women and men, extraverts and introverts). The null hypothesis is that the means of the two populations are the same: µ1 = µ2. The alternative hypothesis is that they are not the same: µ1 ≠ µ2. Again, the test can be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.

Example: Independent-Samples t–Test

Now the health psychologist wants to compare the calorie estimates of people who regularly eat junk food with the estimates of people who rarely eat junk food. S/he believes the difference could come out in either direction so s/he decides to conduct a two-tailed test. S/he collects data from a sample of eight participants who eat junk food regularly and seven participants who rarely eat junk food. The data are as follows:

• Junk food eaters: 180, 220, 150, 85, 200, 170, 150, 190
• Non–junk food eaters: 200, 240, 190, 175, 200, 300, 240

If s/he enters the data into one of the online analysis tools or uses Excel or SPSS, it would indicate that the two- tailed p value for this t score (with 15 − 2 = 13 degrees of freedom) is .015. Because this p value is less than .05, the health psychologist would reject the null hypothesis and conclude that people who eat junk food regularly make lower calorie estimates than people who eat it rarely.

The Analysis of Variance

T-tests are used to compare two means (a sample mean with a population mean, the means of two conditions or two groups). When there are more than two groups or condition means to be compared, the most common null hypothesis test is the analysis of variance (ANOVA). In this section, we look primarily at the one-way ANOVA, which is used for between-subjects designs with a single independent variable.

One-Way ANOVA

The one-way ANOVA is used to compare the means of more than two samples (M1, M2…MG) in a between-subjects design. The null hypothesis is that all the means are equal in the population: µ1= µ2 =…= µG. The alternative hypothesis is that not all the means in the population are equal.

The test statistic for the ANOVA is called F. The reason that F is useful is that we know how it is distributed when the null hypothesis is true. This distribution is unimodal and positively skewed with values that cluster around 1. The precise shape of the distribution depends on both the number of groups and the sample size, and there are degrees of freedom values associated with each of these. The between-groups degrees of freedom is the number of groups minus one: dfB = (G − 1). The within-groups degrees of freedom is the total sample size minus the number of groups: dfW = N − G. Again, knowing the distribution of F when the null hypothesis is true allows us to find the p value.

Statistical software such as Excel and SPSS will compute F and find the p value. If p is equal to or less than .05, then we reject the null hypothesis and conclude that there are differences among the group means in the population. If p is greater than .05, then we retain the null hypothesis and conclude that there is not enough evidence to say that there are differences.

Example: One-Way ANOVA

Imagine that a health psychologist wants to compare the calorie estimates of psychology majors, nutrition majors, and professional dieticians. He collects the following data:

• Psych majors: 200, 180, 220, 160, 150, 200, 190, 200
• Nutrition majors: 190, 220, 200, 230, 160, 150, 200, 210, 195
• Dieticians: 220, 250, 240, 275, 250, 230, 200, 240

The means are 187.50 (SD = 23.14), 195.00 (SD = 27.77), and 238.13 (SD = 22.35), respectively. So it appears that dieticians made substantially more accurate estimates on average. The researcher would almost certainly enter these data into a program such as Excel or SPSS, which would compute F for him or her and find the p value. Table 13.4 shows the output of the one-way ANOVA function in Excel for these data. This table is referred to as an ANOVA table. It shows that MSB is 5,971.88, MSW is 602.23, and their ratio, F, is 9.92. The p value is .0009. Because this value is below .05, the researcher would reject the null hypothesis and conclude that the mean calorie estimates for the three groups are not the same in the population.

ANOVA Elaborations Post Hoc Comparisons

When we reject the null hypothesis in a one-way ANOVA, we conclude that the group means are not all the same in the population. But this can indicate different things. With three groups, it can indicate that all three means are significantly different from each other, or it can indicate that one of the means is significantly different from the other two, but the other two are not significantly different from each other. It could be, for example, that the mean calorie estimates of psychology majors, nutrition majors, and dieticians are all significantly different from each other. Or it could be that the mean for dieticians is significantly different from the means for psychology and nutrition majors, but the means for psychology and nutrition majors are not significantly different from each other. For this reason, statistically significant one-way ANOVA results are typically followed up with a series of post hoc comparisons of selected pairs of group means to determine which are different from which others.

One approach to post hoc comparisons would be to conduct a series of independent-samples t‐tests comparing each group mean to each of the other group means. But there is a problem with this approach. In general, if we conduct a t-test when the null hypothesis is true, we have a 5% chance of mistakenly rejecting the null hypothesis (see Section 13.3 “Additional Considerations” for more on such Type I errors). If we conduct several t‐tests when the null hypothesis is true, the chance of mistakenly rejecting at least one null hypothesis increases with each test we conduct. Thus researchers do not usually make post hoc comparisons using standard t‐tests because there is too great a chance that they will mistakenly reject at least one null hypothesis. Instead, they use one of several modified t-test procedures—among them the Bonferonni procedure, Fisher’s least significant difference (LSD) test, and Tukey’s honestly significant difference (HSD) test. The details of these approaches are beyond the scope of this book, but it is important to understand their purpose. It is to keep the risk of mistakenly rejecting a true null hypothesis to an acceptable level (close to 5%).

Testing Correlation Coefficients

For relationships between quantitative variables, where Pearson’s r (the correlation coefficient) is used to describe the strength of those relationships, the appropriate null hypothesis test is a test of the correlation coefficient. The basic logic is exactly the same as for other null hypothesis tests. In this case, the null hypothesis is that there is no relationship in the population. We can use the Greek lowercase rho (ρ) to represent the relevant parameter: ρ = 0. The alternative hypothesis is that there is a relationship in the population: ρ ≠ 0. As with the t‐ test, this test can be two-tailed if the researcher has no expectation about the direction of the relationship or one-tailed if the researcher expects the relationship to go in a particular direction.

It is possible to use the correlation coefficient for the sample to compute a t score with N − 2 degrees of freedom and then to proceed as for a t‐test. However, because of the way it is computed, the correlation coefficient can also be treated as its own test statistic. The online statistical tools and statistical software such as Excel and SPSS generally compute the correlation coefficient and provide the p value associated with that value. As always, if the p value is equal to or less than .05, we reject the null hypothesis and conclude that there is a relationship between the variables in the population. If the p value is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say there is a relationship in the population.

Example: Test of a Correlation Coefficient

Imagine that the health psychologist is interested in the correlation between people’s calorie estimates and their weight. She has no expectation about the direction of the relationship, so she decides to conduct a two- tailed test. She computes the correlation coefficient for a sample of 22 university students and finds that Pearson’s r is −.21. The statistical software she uses tells her that the p value is .348. It is greater than .05, so she retains the null hypothesis and concludes that there is no relationship between people’s calorie estimates and their weight.

Simple Regression

Regression is a special kind of correlation analysis, but in the case of regression it isn’t the strength of the association that one is interested in but rather how a change in one variable may be accompanied by a change in another variable. For instance, what effect on average does studying 15 minutes more each day have on a student’s GPA? As such, regression is a predictive exercise—we want to predict how a dependent variable will change given a particular change in the independent variable.

In order to estimate these effects, we need to derive a regression equation, which is simply an equation that describes the relationship between the two variables. The general form of a simple regression equation is: y = mx + b. Y is the dependent (outcome) variable, x is the independent variable, m is the slope of the line that describes the relationship between them, and b is a constant that indicates where the line crosses the y axis.

For example, consider the following:

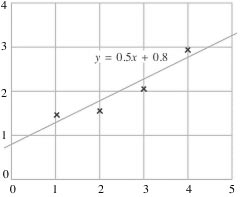
In this case, our dependent variable is predicted by the equation y = 0.5x + 0.8. Let’s suppose that variable x is body satisfaction and variable y is self esteem. If one’s body satisfaction were 5, we would expect one’s self esteem to be 0.5(5) + 0.8 = 3.3.

The way that regression equations are most often used, however, is not for this kind of specific prediction (at least, not in the way just described) but rather they are used to gauge the effect of a change in the independent variable upon the dependent variable. For example, what effect might a one unit increase in body satisfaction have upon one’s level of self esteem? Using the equation above, we would say that a one unit increase in body satisfaction would lead to a 0.5(1) + 0.8 = 1.3 unit increase in self esteem.

Multiple Regression

That which has just been described is called simple regression because there is only one independent variable. Multiple regression works the same way but it is used when you have more than one independent variable. For instance, perhaps you have developed a model (what researchers call equations like these) that has perceived health being a function of exercise frequency, weight, and perceived healthfulness of foods typically consumed. In this case, the formula would be something like: PH = βEF + βW + βHF + b, where each of the “β”s represents a particular coefficient that is applied to each independent variable (like 0.5 was in the previous example). These “betas” tell you the kind of effect a change in one independent variable will have while all the other variables remain constant. So, the bigger the beta coefficient, the bigger the effect upon the dependent variable will be. Suppose the equation were actually PH = 5EF + 2 W + 8HF. A one unit increase in perceived healthfulness of food consumed (HF) will yield an eight unit increase in perceived health, holding the other variables constant. Similarly, a one unit increase in weight (W) should yield a 2 unit increase in PH, and a 1 unit increase in exercise frequency (EF) should yield a 5 unit increase in PH. So, if you wanted to make people feel as though they were healthier, which personal characteristic would you spend your time trying to increase (perhaps through some kind of counselling or therapy)? Based on this equation, if you could get someone to increase their perception that they eat healthy foods, this would have the biggest effect on their overall health perceptions.

One small disclaimer need be said: That’s not exactly how regression works. It is actually based on what are called “standardized values,” but explaining what these are and how they are derived would a) take too long and b) not really add a heck of a lot to the explanation, anyway.

In short, standardizing scores transforms them all into the same unit of measure (actually, standard deviation units) so that they can reasonably be compared; in essence, it turns apples and oranges into apples and apples. That way, when one talks about a “one unit increase” this means the same thing irrespective of whether one variable is measured on a scale from one to four, another in pounds, and another in miles.