It is also useful to be able to describe the characteristics of a distribution more precisely. Here we look at how to do this in terms of two important characteristics: their central tendency and their variability.

Central Tendency

The central tendency of a distribution is its middle—the point around which the scores in the distribution tend to cluster. (Another term for central tendency is average.) Looking back at Figure 9.1, for example, we can see that the self-esteem scores tend to cluster around the values of 20 to 22. Here we will consider the three most common measures of central tendency: the mean, the median, and the mode.

The mean of a distribution (symbolized M) is the sum of the scores divided by the number of scores. It is an average. As a formula, it looks like this:

M=ΣX/N

In this formula, the symbol Σ (the Greek letter sigma) is the summation sign and means to sum across the values of the variable X. N represents the number of scores. The mean is by far the most common measure of central tendency, and there are some good reasons for this. It usually provides a good indication of the central tendency of a distribution, and it is easily understood by most people. In addition, the mean has statistical properties that make it especially useful in doing inferential statistics.

An alternative to the mean is the median. The median is the middle score in the sense that half the scores in the distribution are less than it and half are greater than it. The simplest way to find the median is to organize the scores from lowest to highest and locate the score in the middle. Consider, for example, the following set of seven scores:

8 4 12 14 3 2 3

To find the median, simply rearrange the scores from lowest to highest and locate the one in the middle.

2 3 3 4 8 12 14

In this case, the median is 4 because there are three scores lower than 4 and three scores higher than 4.

When there is an even number of scores, there are two scores in the middle of the distribution, in which case the median is the value halfway between them. For example, if we were to add a score of 15 to the preceding data set, there would be two scores (both 4 and 8) in the middle of the distribution, and the median would be halfway between them (6).

One final measure of central tendency is the mode. The mode is the most frequent score in a distribution. In the self-esteem distribution presented in Table 12.1 and Figure 12.1, for example, the mode is 22. More students had that score than any other. The mode is the only measure of central tendency that can also be used for categorical variables.

In a distribution that is both unimodal and symmetrical, the mean, median, and mode will be very close to each other at the peak of the distribution. In a bimodal or asymmetrical distribution, the mean, median, and mode can be quite different. In a bimodal distribution, the mean and median will tend to be between the peaks, while the mode will be at the tallest peak. In a skewed distribution, the mean will differ from the median in the direction of the skew (i.e., the direction of the longer tail). For highly skewed distributions, the mean can be pulled so far in the direction of the skew that it is no longer a good measure of the central tendency of that distribution. Imagine, for example, a set of four simple reaction times of 200, 250, 280, and 250 milliseconds (ms). The mean is 245 ms. But the addition of one more score of 5,000 ms—perhaps because the participant was not paying attention—would raise the mean to 1,445 ms. Not only is this measure of central tendency greater than 80% of the scores in the distribution, but it also does not seem to represent the behavior of anyone in the distribution very well. This is why researchers often prefer the median for highly skewed distributions (such as distributions of reaction times).

Keep in mind, though, that you are not required to choose a single measure of central tendency in analyzing your data. Each one provides slightly different information, and all of them can be useful.

Measures of Variability

The variability of a distribution is the extent to which the scores vary around their central tendency. Consider the two distributions in Figure 9.4, each of which has the same central tendency. The mean, median, and mode of each distribution are 5. Notice, however, that the distributions differ in terms of their variability. From left to right in Figure 9.4, the observations become less clustered around the centre value.

One simple measure of variability is the range, which is simply the difference between the highest and lowest scores in the distribution. The range of the self-esteem scores in Table 9.1, for example, is the difference between the highest score (24) and the lowest score (15). That is, the range is 24 − 15 = 9. Although the range is easy to compute and understand, it can be misleading when there are outliers. Imagine, for example, an exam on which all the students scored between 90 and 100. It has a range of 10. But if there was a single student who scored 20, the range would increase to 80—giving the impression that the scores were quite variable when in fact only one student differed substantially from the rest.

By far the most common measure of variability is the standard deviation. The standard deviation of a distribution is the average distance between the scores and the mean. The broader the distribution (the more observations diverge from the mean), the higher the standard deviation and the narrower the distribution (the less observations diverge from the mean), the smaller the standard deviation..

Computing the standard deviation involves a slight complication. Specifically, it involves finding the difference between each score and the mean, squaring each difference, finding the mean of these squared differences, and finally finding the square root of that mean. The formula looks like this:

  
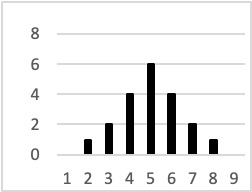
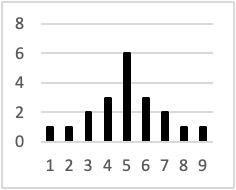
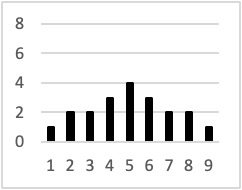
Figure 9.4 Distributions With the Same Mean, Median and Mode and Varying Standard Deviation

Percentile Ranks and z Scores

In many situations, it is useful to have a way to describe the location of an individual score within its distribution. One approach is the percentile rank. The percentile rank of a score is the percentage of scores in the distribution that are lower than that score. Consider, for example, the distribution in Table 12.1. For any score in the distribution, we can find its percentile rank by counting the number of scores in the distribution that are lower than that score and converting that number to a percentage of the total number of scores.

Notice, for example, that five of the students represented by the data in Table 9.1 had self-esteem scores of 23. In this distribution, 32 of the 40 scores (80%) are lower than 23. Thus each of these students has a percentile rank of 80. (It can also be said that they scored “at the 80th percentile.”) Percentile ranks are often used to report the results of standardized tests of ability or achievement. If your percentile rank on a test of verbal ability were 40, for example, this would mean that you scored higher than 40% of the people who took the test.

Another approach is the z score. The z score for a particular individual is the difference between that individual’s score and the mean of the distribution, divided by the standard deviation of the distribution:

z = (X−M)/SD

A z score indicates how far above or below the mean a raw score is, but it expresses this in terms of the standard deviation. For example, in a distribution of intelligence quotient (IQ) scores with a mean of 100 and a standard deviation of 15, an IQ score of 110 would have a z score of (110 − 100) / 15 = +0.67. In other words, a score of 110 is 0.67 standard deviations (approximately two thirds of a standard deviation) above the mean.

Similarly, a raw score of 85 would have a z score of (85 − 100) / 15 = −1.00. In other words, a score of 85 is one standard deviation below the mean.

There are several reasons that z scores are important. Again, they provide a way of describing where an individual’s score is located within a distribution and are sometimes used to report the results of standardized tests. They also provide one way of defining outliers. For example, outliers are sometimes defined as scores that have z scores less than −3.00 or greater than +3.00. In other words, they are defined as scores that are more than three standard deviations from the mean. Finally, z scores play an important role in understanding and computing other statistics, as we will see shortly.