As we have seen throughout this book, most interesting research questions in quantitative social sciences are about statistical relationships between variables. In this section, we revisit the two basic forms of statistical relationship introduced earlier in the book—differences between groups or conditions and relationships between quantitative variables—and we consider how to describe them in more detail.

Differences Between Groups or Conditions

Differences between groups or conditions are usually described in terms of the mean and standard deviation of each group or condition. For example, Thomas Ollendick and his colleagues conducted a study in which they evaluated two one-session treatments for simple phobias in children (Ollendick et al., 2009). They randomly assigned children with an intense fear (e.g., to dogs) to one of three conditions. In the exposure condition, the children actually confronted the object of their fear under the guidance of a trained therapist. In the education condition, they learned about phobias and some strategies for coping with them. In the wait-list control condition, they were waiting to receive a treatment after the study was over. The severity of each child’s phobia was then rated on a 1-to-8 scale by a clinician who did not know which treatment the child had received. (This was one of several dependent variables.) The mean fear rating in the education condition was 4.83 with a standard deviation of 1.52, while the mean fear rating in the exposure condition was 3.47 with a standard deviation of 1.77. The mean fear rating in the control condition was 5.56 with a standard deviation of 1.21. In other words, both treatments worked, but the exposure treatment worked better than the education treatment. As we have seen, differences between group or condition means can be presented in a bar graph.

It is also important to be able to describe the strength of a statistical relationship, which is often referred to as the effect size. The most widely used measure of effect size for differences between group or condition means is called Cohen’s d, which is the difference between the two means divided by the standard deviation:

d = (M1 −M2)/SD

Conceptually, Cohen’s d is the difference between the two means expressed in standard deviation units. (Notice its similarity to a z score, which expresses the difference between an individual score and a mean in standard deviation units.) A Cohen’s d of 0.50 means that the two group means differ by 0.50 standard deviations (half a standard deviation). A Cohen’s d of 1.20 means that they differ by 1.20 standard deviations. But how should we interpret these values in terms of the strength of the relationship or the size of the difference between the means? Table 9.4 presents some guidelines for interpreting Cohen’s d values in psychological research (Cohen, 1992). Values near 0.20 are considered small, values near 0.50 are considered medium, and values near 0.80 are considered large. Thus a Cohen’s d value of 0.50 represents a medium- sized difference between two means, and a Cohen’s d value of 1.20 represents a very large difference in the context of social science research. In the research by Ollendick and his colleagues, there was a large difference (d = 0.82) between the exposure and education conditions.

Cohen’s d is useful because it has the same meaning regardless of the variable being compared or the scale it was measured on. A Cohen’s d of 0.20 means that the two group means differ by 0.20 standard deviations whether we are talking about scores on the Rosenberg Self-Esteem scale, reaction time measured in milliseconds, number of siblings, or diastolic blood pressure measured in millimeters of mercury. Not only does this make it easier for researchers to communicate with each other about their results, it also makes it possible to combine and compare results across different studies using different measures.

Be aware that the term effect size can be misleading because it suggests a causal relationship—that the difference between the two means is an “effect” of being in one group or condition as opposed to another. Imagine, for example, a study showing that a group of exercisers is happier on average than a group of non-exercisers, with an “effect size” of d = 0.35. If the study was an experiment—with participants randomly assigned to exercise and no-exercise conditions—then one could conclude that exercising caused a small to medium-sized increase in happiness. If the study was cross-sectional, however, then one could conclude only that the exercisers were happier than the non-exercisers by a small to medium-sized amount. In other words, simply calling the difference an “effect size” does not make the relationship a causal one.

Correlations Between Quantitative Variables

As we have seen throughout the book, many interesting statistical relationships take the form of correlations between quantitative variables. In general, line graphs are used when the variable on the x‐axis has (or is organized into) a small number of distinct values, such as the four quartiles of the name distribution. Scatterplots are used when the variable on the x‐axis has a large number of values, such as the different possible self-esteem scores.

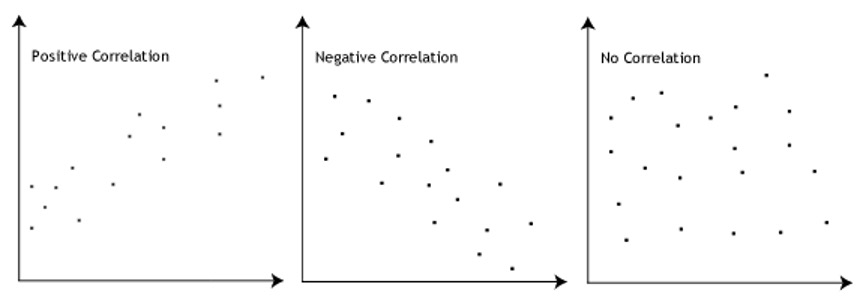
The strength of a correlation between quantitative variables is typically measured using a statistic called Pearson’s r. Its possible values range from −1.00, through zero, to +1.00. A value of 0 means there is no relationship between the two variables, such as the third image in Figure 9.5. In addition to his guidelines for interpreting Cohen’s d, Cohen offered guidelines for interpreting Pearson’s r in psychological research (see Table 9.3). Values near ±.10 are considered small, values near ± .30 are considered medium, and values near ±.50 are considered large. Notice that the sign of Pearson’s r is unrelated to its strength. Pearson’s r values of +.30 and −.30, for example, are equally strong; it is just that one represents a moderate positive relationship and the other a moderate negative relationship. Like Cohen’s d, Pearson’s r is also referred to as a measure of “effect size” even though the relationship may not be a causal one.

There are two common situations in which the value of Pearson’s r can be misleading. One is when the relationship under study is nonlinear. This means that it is important to make a scatterplot and confirm that a relationship is approximately linear before using Pearson’s r (or by transforming variables, which is beyond the scope of this text). The other is when one or both of the variables have a limited range in the sample relative to the population. This problem is referred to as restriction of range. Assume, for example, that there is a strong negative correlation between people’s age and their enjoyment of hip hop music. However, if we were to collect data only from 18- to 24-year-olds, then the relationship might seem to be quite weak (i.e., enjoyment of hip hop doesn’t vary much). In this case, Pearson’s r for this restricted range of ages might be zero, even though the relationship holds across all ages. It is a good idea, therefore, to design studies to avoid restriction of range. For example, if age is one of your primary variables, then you can plan to collect data from people of a wide range of ages. Because restriction of range is not always anticipated or easily avoidable, however, it is good practice to examine your data for possible restriction of range and to interpret Pearson’s r in light of it.